Inference for ranks with applications to mobility across neighborhoods and academic achievement across countries

What is this research about and why did you do it?

Rankings (e.g., of hospitals, political parties, schools) are ubiquitous. These are often based on estimated features of the objects to be ranked (e.g., hospital or school performance, a party’s vote share). As a result, there may be considerable uncertainty concerning the true ranking. An important example of contemporary interest is the ranking of neighbourhoods by measures of intergenerational mobility to study which neighbourhoods provide relatively more opportunities for children to rise out of poverty. 

‍

How did you answer this question?

In this paper, we develop confidence sets for ranks which, for each neighbourhood, indicate the range in which its true rank lies with high probability. We also provide confidence sets containing the neighbourhoods that truly are among the best/worst with high probability. 

We apply our theoretical results to re-examine the rankings of neighbourhoods in the United States by intergenerational mobility.

‍

What did you find?

Rankings of neighbourhoods by measures of intergenerational mobility differ substantially in the degree to which they are informative. Specifically, the confidence intervals for the ranks are fairly narrow, and thus informative, when using so-called correlational measures of mobility, but they can be very wide, and thus uninformative, when using so-called movers measures of mobility.

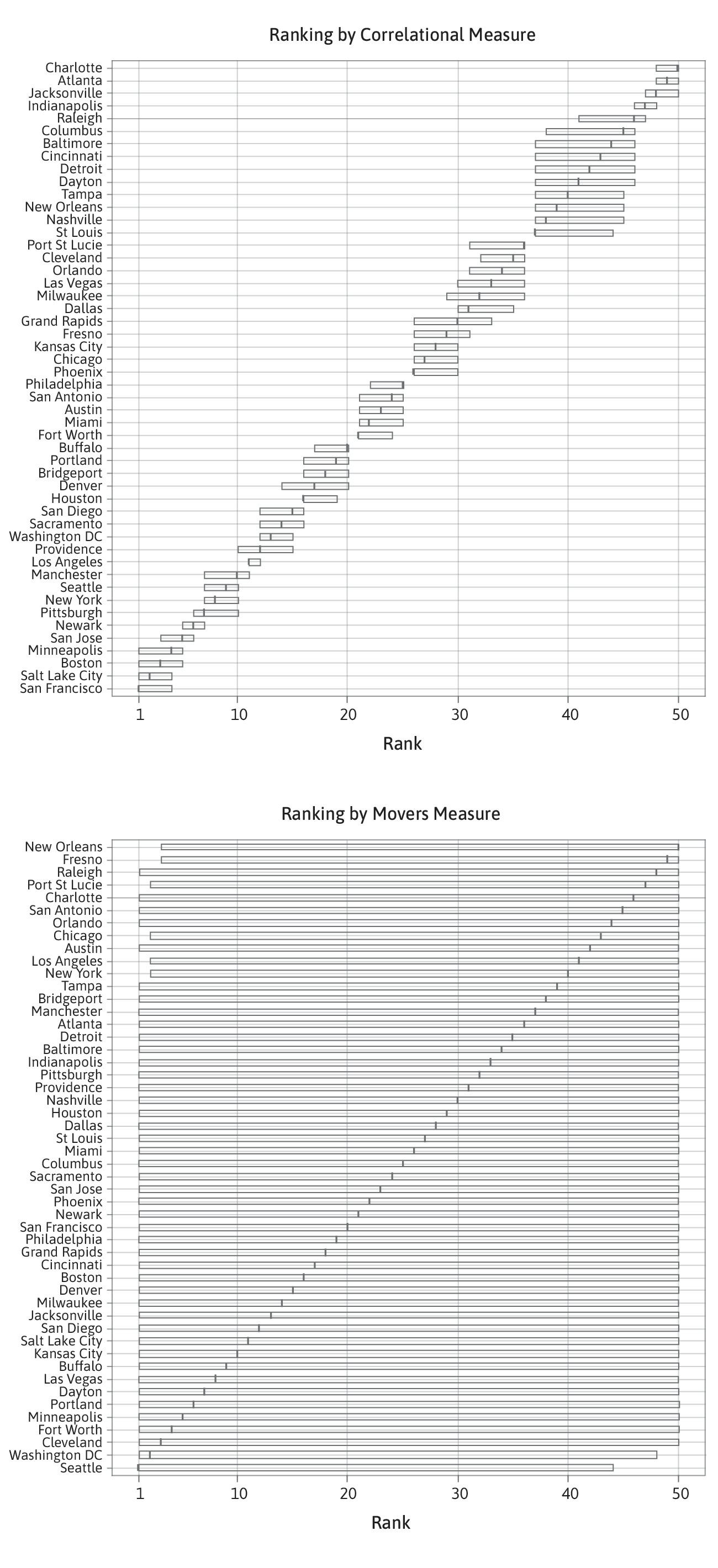
Ranking of the 50 most populous commuting zones in the U.S. by two different measures of intergenerational mobility (“correlational” and “movers”) together with 95% simultaneous confidence intervals for the ranks. The left panel shows a relatively informative ranking with narrow confidence intervals; the right panel shows an uninformative ranking with very wide confidence intervals. “Correlational” estimates measure the correlation between children’s and parents’ rank in their respective income distributions. “Movers” estimates measure the causal impact of a child spending an additional year in a given commuting zone on their adult income.

‍

What implications does this have for the research on wealth concentration or economic inequality?

Rankings of neighbourhoods by intergenerational mobility have been used to study how “bad” neighbourhoods can be improved by changing some of their attributes to become more like those of the “good” neighbourhoods. Our research cautions that such findings may not be reliable when the rankings are too uninformative to distinguish “good” from “bad” neighbourhoods.

‍

What are the next steps in your agenda?

The next step is to develop statistical methods that reliably identify characteristics that separate “good” from “bad” neighbourhood. 

‍

Citation and related resources

This paper can be cited as: Mogstad, M., Romano, J., Shaikh, A. and Wilhelm, D. (2022) 'Inference for Ranks with Applications to Mobility across Neighborhoods and Academic Achievement across Countries'. Review of Economic Studies (forthcoming). A pre-publication version is available from the NBER website.

Related resource:

• R package for the computation of confidence sets for rank