Inequality as experienced difference: a reformulation of the Gini coefficient
What is this research about and why did you do it?
UCL students in the introductory economics module ran into a problem. Using the standard (e.g. Wolfram) algorithm for calculating the Gini coefficient on the small population datasets we had provided, they found that when all wealth was held by a single individual the Gini did not equal 1 (as should be the case) but instead fell far short of that. The glitch with the algorithm stimulated us to ask a broader question: Is there an inequality measure that both captures how people experience economic disparities and independently of the number of wealth holders, is not downward-biased?
How did you answer this question?
Inequality is typically measured as the degree of dispersion of a distribution of individual attributes, say, wealth, as is captured for example by the Lorenz curve, and its associated statistic, the Gini coefficient. But both the economics and social psychology of experienced inequality are better expressed by differences between an individual and others. There is a natural way to do this using the standard definition of the Gini coefficient as one half the mean difference among individuals, relative to the population mean wealth.
What did you find?
We found that reformulating the Gini coefficient as a measure of experienced inequality on a complete social network yields a computational algorithm that irrespective of population size varies from 0 (no differences among individuals) to 1 (one individual owns all the wealth).
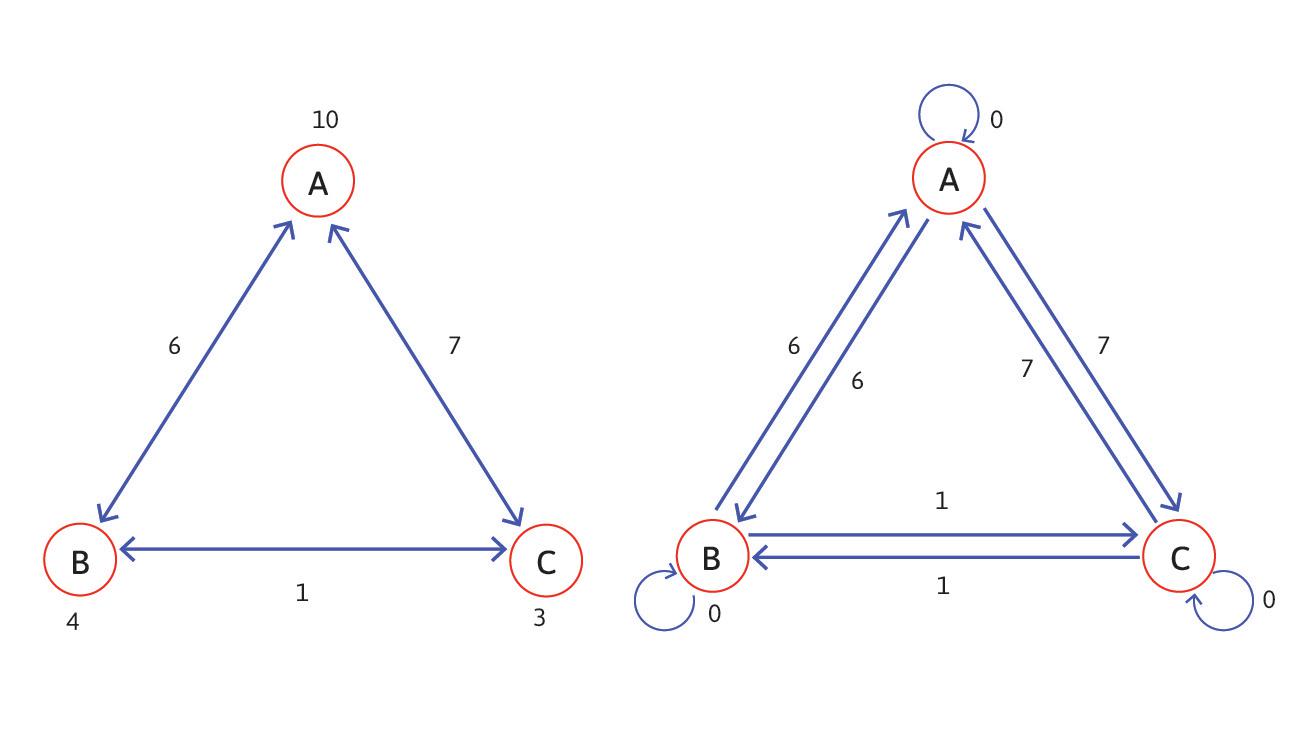
Two representations of wealth inequality. The numbers at the nodes are wealth and along the edges are wealth differences. Using the network representation in the left panel G = 0.412. On the right, the conventional algorithm counts all the edges shown and returns G = 0.274 which understates inequality because it includes the three “self-on-self” zero differences.
What implications does this have for the research on, and teaching of wealth concentration or economic inequality?
The network representation of inequality and the Gini coefficient allows consistent measurement of inequality even for very small data sets used in many fields, and also in undergraduate teaching, where our focus on the edges of the network not the nodes prompts students to think about how inequality feels not only economically, but also socially and psychologically.
What are the next steps in your agenda?
We are participating in a project at the Santa Fe Institute on network structure and wealth inequality in more than 50 small scale societies to explore how experienced wealth inequality depends on network structure.
Citation and related resources
This paper can be cited as follows: Bowles, S. and Carlin, W. (2020) 'Inequality as Experienced Difference: A Reformulation of the Gini Coefficient.' Economics Letters, 186, pp. 1-3.
Related literature:
- Fochesato, M., Bogaard, A. and Bowles, S. (2019) 'Measuring Ancient Inequality: The Challenges of Comparability, Bias, and Precision.' Antiquity, 93(370), pp. 853-69
Related resources:
- the Gini coefficient explained for 1st year students can be found in Unit 5 of CORE's free ebook The Economy
- Gini realized (in 1914) that there are many ways to measure inequality. For a lively debate (2021) on the interpretation of the Gini coefficient including Debraj Ray, Rajiv Sethi, S. Subramanian, Wendy Carlin and Sam Bowles, see: https://debrajray.com/2021/10/01/a-discussion-of-the-gini-coefficient/





